Γυμνάσιο MBOU №17 Ivanov

« Modulo Equations»
Μεθοδική ανάπτυξη

Συντάχθηκε

μαθηματικός

Lebedeva N.V.

20010

Επεξηγηματικό σημείωμα

κεφάλαιο 1 Εισαγωγή

Ενότητα 2. Κύρια χαρακτηριστικά Ενότητα 3. Γεωμετρική ερμηνεία της έννοιας του συντελεστή ενός αριθμού Ενότητα 4. Γράφημα της συνάρτησης y = |x| Ενότητα 5 Συμβάσεις

Κεφάλαιο 2

Ενότητα 1. Εξισώσεις της μορφής |F(х)| = m (πρωτόζωα) Ενότητα 2. Εξισώσεις της μορφής F(|х|) = m Ενότητα 3. Εξισώσεις της μορφής |F(х)| = G(x) Ενότητα 4. Εξισώσεις της μορφής |F(х)| = ± F(x) (όμορφο) Ενότητα 5. Εξισώσεις της μορφής |F(х)| = |G(x)| Ενότητα 6. Παραδείγματα επίλυσης μη τυπικών εξισώσεων Ενότητα 7. Εξισώσεις της μορφής |F(х)| + |G(x)| = 0 Ενότητα 8. Εξισώσεις της μορφής |а 1 x ± v 1 | ± |a 2 x ± σε 2 | ± …|a n x ± σε n | = m Ενότητα 9. Εξισώσεις που περιέχουν πολλαπλές ενότητες

Κεφάλαιο 3. Παραδείγματα επίλυσης διαφόρων εξισώσεων με συντελεστή.

Τμήμα 1. Τριγωνομετρικές εξισώσεις Τομέας 2 εκθετικές εξισώσεις Ενότητα 3 Λογαριθμικές Εξισώσεις Ενότητα 4. Ανορθολογικές Εξισώσεις Ενότητα 5. Εργασίες προηγμένης πολυπλοκότητας Απαντήσεις στις ασκήσεις Βιβλιογραφία

Επεξηγηματικό σημείωμα.

Η έννοια της απόλυτης τιμής (μέτρο) ενός πραγματικού αριθμού είναι ένα από τα ουσιαστικά χαρακτηριστικά του. Αυτή η έννοια χρησιμοποιείται ευρέως σε διάφορους κλάδους των φυσικών, μαθηματικών και τεχνικών επιστημών. Στην πρακτική της διδασκαλίας ενός μαθήματος μαθηματικών σε Λύκειοσύμφωνα με το Πρόγραμμα του Υπουργείου Άμυνας της Ρωσικής Ομοσπονδίας, η έννοια της "απόλυτης τιμής ενός αριθμού" εμφανίζεται επανειλημμένα: στην 6η τάξη, εισάγεται ένας ορισμός της ενότητας, γεωμετρική σημασία; στην 8η τάξη σχηματίζεται η έννοια του απόλυτου λάθους, εξετάζεται η λύση των απλούστερων εξισώσεων και ανισώσεων που περιέχουν το μέτρο, οι ιδιότητες της αριθμητικής τετραγωνική ρίζα; στην 11η τάξη, η έννοια βρίσκεται στην ενότητα «Ρίζα nου βαθμού."Η διδακτική εμπειρία δείχνει ότι οι μαθητές συχνά αντιμετωπίζουν δυσκολίες στην επίλυση εργασιών που απαιτούν γνώση αυτού του υλικού και συχνά παραλείπουν χωρίς να αρχίσουν να ολοκληρώνουν. Στα κείμενα των εργασιών εξέτασης για το μάθημα της 9ης και της 11ης τάξης περιλαμβάνονται και παρόμοιες εργασίες. Επιπλέον, οι απαιτήσεις που επιβάλλουν τα πανεπιστήμια στους αποφοίτους σχολείων είναι διαφορετικές, δηλαδή, υψηλότερου επιπέδου από τις απαιτήσεις του σχολικού προγράμματος σπουδών. Για τη ζωή σε σύγχρονη κοινωνίαπολύ σημαντική είναι η διαμόρφωση ενός μαθηματικού στυλ σκέψης, που εκδηλώνεται σε ορισμένες νοητικές δεξιότητες. Στη διαδικασία επίλυσης προβλημάτων με ενότητες, απαιτείται η ικανότητα εφαρμογής τεχνικών όπως η γενίκευση και η συγκεκριμενοποίηση, η ανάλυση, η ταξινόμηση και η συστηματοποίηση, η αναλογία. Η λύση τέτοιων εργασιών σας επιτρέπει να ελέγξετε τις γνώσεις των κύριων τμημάτων του σχολικού μαθήματος, το επίπεδο λογική σκέψη, αρχικές ερευνητικές δεξιότητες. Αυτή η εργασία είναι αφιερωμένη σε μία από τις ενότητες - τη λύση των εξισώσεων που περιέχουν το μέτρο. Αποτελείται από τρία κεφάλαια. Το πρώτο κεφάλαιο εισάγει τις βασικές έννοιες και τους σημαντικότερους θεωρητικούς υπολογισμούς. Το δεύτερο κεφάλαιο προτείνει εννέα βασικούς τύπους εξισώσεων που περιέχουν την ενότητα, εξετάζει μεθόδους για την επίλυσή τους και αναλύει παραδείγματα διαφορετικά επίπεδαδυσκολίες. Το τρίτο κεφάλαιο προσφέρει πιο σύνθετες και μη τυπικές εξισώσεις (τριγωνομετρικές, εκθετικές, λογαριθμικές και παράλογες). Για κάθε τύπο εξισώσεων υπάρχουν ασκήσεις για ανεξάρτητη λύση (επισυνάπτονται απαντήσεις και οδηγίες). Ο κύριος σκοπός αυτής της εργασίας είναι να παρέχει μεθοδολογική βοήθειαεκπαιδευτικών στην προετοιμασία για τα μαθήματα και στη διοργάνωση προαιρετικών μαθημάτων. Το υλικό μπορεί να χρησιμοποιηθεί και ως εκπαιδευτικό βοήθημα για μαθητές Λυκείου. Οι εργασίες που προσφέρονται στην εργασία είναι ενδιαφέρουσες και δεν είναι πάντα εύκολο να επιλυθούν, κάτι που σας επιτρέπει να το κάνετε κίνητρα μάθησηςοι μαθητές πιο συνειδητοποιημένοι, δοκιμάζουν τις ικανότητές τους, βελτιώνουν το επίπεδο προετοιμασίας των αποφοίτων σχολείων για την είσοδο στα πανεπιστήμια. Μια διαφοροποιημένη επιλογή των προτεινόμενων ασκήσεων συνεπάγεται μια μετάβαση από το αναπαραγωγικό επίπεδο αφομοίωσης του υλικού στο δημιουργικό, καθώς και την ευκαιρία να διδάξουν πώς να εφαρμόζουν τις γνώσεις τους στην επίλυση μη τυπικών προβλημάτων.

Κεφάλαιο 1 Εισαγωγή.

Ενότητα 1. Προσδιορισμός της απόλυτης τιμής .

Ορισμός : Η απόλυτη τιμή (μέτρο) ενός πραγματικού αριθμού έναονομάζεται μη αρνητικός αριθμός: έναή -ένα. Ονομασία: │ ένα │ Η καταχώρηση έχει ως εξής: «μονάδα του αριθμού α» ή «απόλυτη τιμή του αριθμού α»

│ a εάν a > 0

│a│ = │ 0 εάν a = 0 (1)

│ - α, αν α
Παραδείγματα: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Ανάπτυξη ενότητας έκφρασης:

α) │x - 8│ αν x > 12 β) │2x + 3│ αν x ≤ -2 │x - 8│= x - 8 │ 2x + 3│= - 2x - 3

Ενότητα 2. Βασικές ιδιότητες.

Εξετάστε τις βασικές ιδιότητες της απόλυτης τιμής. Ιδιοκτησία #1: Οι αντίθετοι αριθμοί έχουν ίσες ενότητες, δηλ. │а│=│-а│Ας δείξουμε την ορθότητα της ισότητας. Ας γράψουμε τον ορισμό του αριθμού - ένα : │- α│= (2) Ας συγκρίνουμε τα σύνολα (1) και (2). Προφανώς, οι ορισμοί των απόλυτων τιμών των αριθμών ένακαι - ένααγώνας. Συνεπώς, │а│=│-а│
Όταν εξετάζουμε τις ακόλουθες ιδιότητες, περιοριζόμαστε στη διατύπωσή τους, αφού η απόδειξή τους δίνεται Ιδιοκτησία #2: Η απόλυτη τιμή του αθροίσματος ενός πεπερασμένου αριθμού πραγματικών αριθμών δεν υπερβαίνει το άθροισμα των απόλυτων τιμών των όρων: Ιδιοκτησία #3: Η απόλυτη τιμή της διαφοράς μεταξύ δύο πραγματικών αριθμών δεν υπερβαίνει το άθροισμα των απόλυτων τιμών τους: │а - в│ ≤│а│+│в│ Ιδιοκτησία #4: Η απόλυτη τιμή του γινομένου ενός πεπερασμένου αριθμού πραγματικών αριθμών είναι ίση με το γινόμενο των απόλυτων τιμών των παραγόντων: │а · │=│а│·│в│ Ιδιοκτησία #5: Η απόλυτη τιμή του πηλίκου των πραγματικών αριθμών είναι ίση με το πηλίκο των απόλυτων τιμών τους:

Ενότητα 3. Γεωμετρική ερμηνεία της έννοιας του συντελεστή ενός αριθμού.

Κάθε πραγματικός αριθμός μπορεί να συσχετιστεί με ένα σημείο στην αριθμητική γραμμή, το οποίο θα είναι μια γεωμετρική αναπαράσταση αυτού του πραγματικού αριθμού. Κάθε σημείο της αριθμογραμμής αντιστοιχεί στην απόστασή του από την αρχή, δηλ. το μήκος του τμήματος από την αρχή έως το δεδομένο σημείο. Αυτή η απόσταση θεωρείται πάντα ως μη αρνητική τιμή. Επομένως, το μήκος του αντίστοιχου τμήματος θα είναι η γεωμετρική ερμηνεία της απόλυτης τιμής του δεδομένου πραγματικού αριθμού

Η παρουσιαζόμενη γεωμετρική απεικόνιση επιβεβαιώνει ξεκάθαρα την ιδιότητα Νο. 1, δηλ. μέτρο των αντίθετων αριθμών είναι ίσα. Από εδώ γίνεται εύκολα κατανοητή η εγκυρότητα της ισότητας: │x - a│= │a - x│. Γίνεται επίσης πιο προφανές να λύσουμε την εξίσωση │х│= m, όπου m ≥ 0, δηλαδή x 1,2 = ± m. Παραδείγματα: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
x 1,2 = 2; τέσσερις

Ενότητα 4. Γράφημα της συνάρτησης y \u003d │х│

Ο τομέας αυτής της συνάρτησης είναι όλοι οι πραγματικοί αριθμοί.

Ενότητα 5. Σύμβολα.

Στο μέλλον, κατά την εξέταση παραδειγμάτων επίλυσης εξισώσεων, θα χρησιμοποιηθούν τα ακόλουθα. συµβάσεις: ( - σύμβολο συστήματος [ - σύμβολο ορισμού Κατά την επίλυση ενός συστήματος εξισώσεων (ανισώσεις), βρίσκεται η τομή των λύσεων των εξισώσεων (ανισώσεων) που περιλαμβάνονται στο σύστημα. Κατά την επίλυση ενός συνόλου εξισώσεων (ανισώσεις), βρίσκεται μια ένωση λύσεων των εξισώσεων (ανισώσεων) που περιλαμβάνονται στο σύνολο.

Κεφάλαιο 2

Σε αυτό το κεφάλαιο, θα εξετάσουμε αλγεβρικούς τρόπους επίλυσης εξισώσεων που περιέχουν μία ή περισσότερες ενότητες.

Ενότητα 1. Εξισώσεις της μορφής │F (х) │= m

Μια εξίσωση αυτού του τύπου ονομάζεται απλούστερη. Έχει λύση αν και μόνο αν m ≥ 0. Με τον ορισμό του συντελεστή, η αρχική εξίσωση είναι ισοδύναμη με το συνδυασμό δύο εξισώσεων: │ φά(x)│=Μ
Παραδείγματα:
№1. Λύστε την εξίσωση: │7x - 2│= 9


Απάντηση: x 1 = - 1; Χ 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 + 3x = 0 x 1 = -1; x 2 \u003d -2 x (x + 3) \u003d 0 x 1 \u003d 0; x 2 = -3 Απάντηση: το άθροισμα των ριζών είναι - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 - 5x 2 = 0 x 4 - 5x 2 + 4 = 0 x 2 (x 2 - 5) = 0 δηλώνει x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – και οι δύο τιμές ικανοποιούν την συνθήκη m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Απάντηση: ο αριθμός των ριζών της εξίσωσης 7. Γυμνάσια:
№1. Λύστε την εξίσωση και υποδείξτε το άθροισμα των ριζών: │x - 5│= 3 №2 . Λύστε την εξίσωση και υποδείξτε τη μικρότερη ρίζα: │x 2 + x │ \u003d 0 №3 . Λύστε την εξίσωση και υποδείξτε τη μεγαλύτερη ρίζα: │x 2 - 5x + 4 │ \u003d 4 №4 .Λύστε την εξίσωση και υποδείξτε ολόκληρη ρίζα: │2x 2 - 7x + 6│= 1 №5 .Λύστε την εξίσωση και υποδείξτε τον αριθμό των ριζών: │x 4 - 13x 2 + 50 │ = 14

Ενότητα 2. Εξισώσεις της μορφής F(│х│) = m

Το όρισμα συνάρτησης στην αριστερή πλευρά βρίσκεται κάτω από το σύμβολο modulo, ενώ η δεξιά πλευρά είναι ανεξάρτητη από τη μεταβλητή. Ας εξετάσουμε δύο τρόπους επίλυσης εξισώσεων αυτού του τύπου. 1 τρόπος:Εξ ορισμού της απόλυτης τιμής, η αρχική εξίσωση είναι ισοδύναμη με το σύνολο δύο συστημάτων. Σε καθένα από τα οποία επιβάλλεται μια συνθήκη στην έκφραση υπομονάδας. φά(│х│) =Μ
Εφόσον η συνάρτηση F(│х│) είναι άρτια σε ολόκληρο το πεδίο ορισμού, οι ρίζες των εξισώσεων F(х) = m και F(-х) = m είναι ζεύγη αντίθετων αριθμών. Επομένως, αρκεί να λύσουμε ένα από τα συστήματα (όταν εξετάζουμε τα παραδείγματα με αυτόν τον τρόπο, θα δοθεί η λύση ενός συστήματος). 2 τρόπος:Εφαρμογή της μεθόδου εισαγωγής νέας μεταβλητής. Στην περίπτωση αυτή εισάγεται ο προσδιορισμός │х│= a, όπου a ≥ 0. Αυτή η μέθοδοςλιγότερο ογκώδης στο σχεδιασμό.
Παραδείγματα: №1 . Λύστε την εξίσωση: 3x 2 - 4│x│ = - 1 Ας χρησιμοποιήσουμε την εισαγωγή μιας νέας μεταβλητής. Σημειώστε │x│= a, όπου a ≥ 0. Παίρνουμε την εξίσωση 3a 2 - 4a + 1 = 0 D = 16 - 12 = 4 a 1 = 1 a 2 = 1 / 3 Επιστρέφουμε στην αρχική μεταβλητή: │x │ = 1 και │х│= 1/3. Κάθε εξίσωση έχει δύο ρίζες. Απάντηση: x 1 = 1; Χ 2 = - 1; Χ 3 = 1 / 3 ; Χ 4 = - 1 / 3 . №2. Λύστε την εξίσωση: 5x 2 + 3│x│- 1 \u003d 1 / 2 │x│ + 3x 2
Ας βρούμε τη λύση του συστήματος του πρώτου συνόλου: 4x 2 + 5x - 2 \u003d 0 D \u003d 57 x 1 \u003d -5 + √57 / 8 x 2 \u003d -5-√57 / 8 Σημειώστε ότι το x 2 κάνει δεν ικανοποιεί τη συνθήκη x ≥ 0. Με τη λύση το δεύτερο σύστημα θα είναι ο αντίθετος αριθμός x 1 . Απάντηση: x 1 = -5+√57 / 8 ; Χ 2 = 5-√57 / 8 .№3 . Λύστε την εξίσωση: x 4 - │х│= 0 Σημειώστε │х│= a, όπου a ≥ 0. Παίρνουμε την εξίσωση a 4 - a \u003d 0 a (a 3 - 1) \u003d 0 a 1 \u003d 0 a 2 \u003d 1 Επιστρέφουμε στην αρχική μεταβλητή: │х│=0 και │х│= 1 x = 0; ± 1 Απάντηση: x 1 = 0; Χ 2 = 1; Χ 3 = - 1.
Γυμνάσια: №6. Λύστε την εξίσωση: 2│х│ - 4.5 = 5 - 3/8 │х│ №7 . Λύστε την εξίσωση, στην απάντηση υποδείξτε τον αριθμό των ριζών: 3x 2 - 7│x│ + 2 = 0 №8 . Λύστε την εξίσωση, στην απάντηση δώστε τις ολόκληρες λύσεις: x 4 + │х│ - 2 = 0

Ενότητα 3. Εξισώσεις της μορφής │F(х)│ = G(х)

Η δεξιά πλευρά μιας εξίσωσης αυτού του τύπου εξαρτάται από μια μεταβλητή και, επομένως, έχει μια λύση εάν και μόνο εάν η δεξιά πλευρά είναι μια συνάρτηση G(x) ≥ 0. Η αρχική εξίσωση μπορεί να λυθεί με δύο τρόπους: 1 τρόπος:Πρότυπο, βασίζεται στην αποκάλυψη της ενότητας με βάση τον ορισμό της και συνίσταται σε μια ισοδύναμη μετάβαση στο συνδυασμό δύο συστημάτων. │ φά(x)│ =σολ(Χ)

Είναι λογικό να χρησιμοποιείται αυτή η μέθοδος στην περίπτωση μιας μιγαδικής έκφρασης για τη συνάρτηση G(x) και μιας λιγότερο σύνθετης έκφρασης για τη συνάρτηση F(x), αφού υποτίθεται ότι επιλύει ανισώσεις με τη συνάρτηση F(x). 2 τρόπος:Συνίσταται στη μετάβαση σε ένα ισοδύναμο σύστημα στο οποίο επιβάλλεται μια προϋπόθεση στη δεξιά πλευρά. │ φά(Χ)│= σολ(Χ)

Αυτή η μέθοδος είναι πιο βολική στη χρήση εάν η έκφραση για τη συνάρτηση G(x) είναι λιγότερο περίπλοκη από τη συνάρτηση F(x), δεδομένου ότι η λύση της ανισότητας G(x) ≥ 0. Επιπλέον, στην περίπτωση από πολλές ενότητες, αυτή η μέθοδος συνιστάται για χρήση της δεύτερης επιλογής. Παραδείγματα: №1. Λύστε την εξίσωση: │x + 2│= 6 -2x
(1 τρόπος) Απάντηση: x = 1 1 / 3 №2.
│x 2 - 2x - 1 │ \u003d 2 (x + 1)
(2 τρόπος) Απάντηση: Το γινόμενο των ριζών είναι 3.
№3. Λύστε την εξίσωση, στην απάντηση γράψτε το άθροισμα των ριζών:
│x - 6 │ \u003d x 2 - 5x + 9

Απάντηση: το άθροισμα των ριζών είναι 4.
Γυμνάσια: №9. │x + 4│= - 3x №10. Λύστε την εξίσωση, στην απάντηση υποδείξτε τον αριθμό των λύσεων: │x 2 + x - 1 │ \u003d 2x - 1 №11 . Λύστε την εξίσωση, στην απάντηση υποδείξτε το γινόμενο των ριζών: │x + 3 │ \u003d x 2 + x - 6

Ενότητα 4. Εξισώσεις της μορφής │F(x)│= F(x) και │F(x)│= - F(x)

Οι εξισώσεις αυτού του τύπου αποκαλούνται μερικές φορές «όμορφες». Δεδομένου ότι η δεξιά πλευρά των εξισώσεων εξαρτάται από τη μεταβλητή, υπάρχουν λύσεις εάν και μόνο εάν η δεξιά πλευρά είναι μη αρνητική. Επομένως, οι αρχικές εξισώσεις είναι ισοδύναμες με τις ανισότητες:
│F(x)│= F(x) F(x) ≥ 0 και │F(x)│= - F(x) F(x) Παραδείγματα: №1 . Λύστε την εξίσωση, στην απάντηση υποδείξτε τη μικρότερη ακέραια ρίζα: │5x - 3│ \u003d 5x - 3 5x - 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Απάντηση: x = 1№2. Λύστε την εξίσωση, στην απάντηση υποδείξτε το μήκος του κενού: │x 2 - 9 │ \u003d 9 - x 2 x 2 - 9 ≤ 0 (x - 3) (x + 3) ≤ 0 [- 3; 3] Απάντηση: το μήκος του κενού είναι 6.№3 . Λύστε την εξίσωση, στην απάντηση υποδείξτε τον αριθμό των ακέραιων λύσεων: │2 + x - x 2 │ = 2 + x - x 2 2 + x - x 2 ≥ 0 x 2 - x - 2 ≤ 0 [- 1; 2] Απάντηση: 4 ολόκληρες λύσεις.№4 . Λύστε την εξίσωση, δώστε την απάντησή σας μεγαλύτερη ρίζα:
│4 - x -
│= 4 – x –
x 2 - 5x + 5 \u003d 0 D \u003d 5 x 1,2 \u003d
≈ 1,4

Απάντηση: x = 3.

Γυμνάσια: №12. Λύστε την εξίσωση, στην απάντηση δώστε ολόκληρη τη ρίζα: │x 2 + 6x + 8 │= x 2 + 6x + 8 №13. Λύστε την εξίσωση, στην απάντηση υποδείξτε τον αριθμό των ακέραιων λύσεων: │13x - x 2 - 36│+ x 2 - 13x + 36 = 0 №14. Λύστε την εξίσωση, στην απάντηση υποδείξτε έναν ακέραιο που δεν είναι η ρίζα της εξίσωσης:

Ενότητα 5. Εξισώσεις της μορφής │F(x)│= │G(x)│

Δεδομένου ότι και οι δύο πλευρές της εξίσωσης είναι μη αρνητικές, η λύση περιλαμβάνει την εξέταση δύο περιπτώσεων: οι εκφράσεις υπομονάδας έχουν ίσο ή αντίθετο πρόσημο. Επομένως, η αρχική εξίσωση είναι ισοδύναμη με τον συνδυασμό δύο εξισώσεων: │ φά(Χ)│= │ σολ(Χ)│
Παραδείγματα: №1. Λύστε την εξίσωση, στην απάντηση υποδείξτε ολόκληρη τη ρίζα: │x + 3│ \u003d │2x - 1│
Απάντηση: ακέραια ρίζα x = 4.№2. Λύστε την εξίσωση: │ x - x 2 - 1│ \u003d │2x - 3 - x 2 │
Απάντηση: x = 2.№3 . Λύστε την εξίσωση, στην απάντηση να αναφέρετε το γινόμενο των ριζών:




Οι ρίζες της εξίσωσης 4x 2 + 2x - 1 \u003d 0 x 1,2 \u003d - 1±√5 / 4 Απάντηση: το γινόμενο των ριζών είναι 0,25. Γυμνάσια: №15 . Λύστε την εξίσωση, στην απάντηση υποδείξτε ολόκληρη τη λύση: │x 2 - 3x + 2│ \u003d │x 2 + 6x - 1│ №16. Λύστε την εξίσωση, στην απάντηση υποδείξτε τη μικρότερη ρίζα: │5x - 3│=│7 - x│ №17 . Λύστε την εξίσωση, στην απάντηση γράψτε το άθροισμα των ριζών:

Ενότητα 6. Παραδείγματα επίλυσης μη τυπικών εξισώσεων

Σε αυτή την ενότητα, εξετάζουμε παραδείγματα μη τυπικών εξισώσεων, στη λύση των οποίων η απόλυτη τιμή της έκφρασης αποκαλύπτεται εξ ορισμού. Παραδείγματα:

№1. Λύστε την εξίσωση, στην απάντηση υποδείξτε το άθροισμα των ριζών: x │x│- 5x - 6 \u003d 0
Απάντηση: το άθροισμα των ριζών είναι 1 №2. . Λύστε την εξίσωση, στην απάντηση υποδείξτε τη μικρότερη ρίζα: x 2 - 4x
- 5 = 0
Απάντηση: μικρότερη ρίζα x = - 5. №3. Λύστε την εξίσωση:

Απάντηση: x = -1. Γυμνάσια: №18. Λύστε την εξίσωση και γράψτε το άθροισμα των ριζών: x │3x + 5│= 3x 2 + 4x + 3
№19. Λύστε την εξίσωση: x 2 - 3x \u003d

№20. Λύστε την εξίσωση:

Ενότητα 7. Εξισώσεις της μορφής │F(x)│+│G(x)│=0

Είναι εύκολο να δούμε ότι στην αριστερή πλευρά μιας εξίσωσης αυτού του τύπου, το άθροισμα των μη αρνητικών μεγεθών. Επομένως, η αρχική εξίσωση έχει λύση εάν και μόνο εάν και οι δύο όροι είναι ταυτόχρονα ίσοι με μηδέν. Η εξίσωση είναι ισοδύναμη με το σύστημα των εξισώσεων: │ φά(Χ)│+│ σολ(Χ)│=0
Παραδείγματα: №1 . Λύστε την εξίσωση:
Απάντηση: x = 2. №2. Λύστε την εξίσωση: Απάντηση: x = 1. Γυμνάσια: №21. Λύστε την εξίσωση: №22 . Λύστε την εξίσωση, στην απάντηση γράψτε το άθροισμα των ριζών: №23 . Λύστε την εξίσωση, στην απάντηση να αναφέρετε τον αριθμό των λύσεων:

Ενότητα 8. Εξισώσεις της φόρμας

Για την επίλυση εξισώσεων αυτού του τύπου χρησιμοποιείται η μέθοδος των διαστημάτων. Αν λυθεί με διαδοχική επέκταση μονάδων, τότε παίρνουμε nσύνολα συστημάτων, το οποίο είναι πολύ δυσκίνητο και άβολο. Εξετάστε τον αλγόριθμο της μεθόδου διαστήματος: 1). Εύρεση μεταβλητών τιμών Χ, για την οποία κάθε ενότητα είναι ίση με μηδέν (μηδενικές εκφράσεις υπομονάδας):
2). Οι τιμές που βρέθηκαν σημειώνονται σε μια αριθμητική γραμμή, η οποία χωρίζεται σε διαστήματα (ο αριθμός των διαστημάτων, αντίστοιχα, είναι ίσος με n+1 ) 3). Προσδιορίστε με ποιο σύμβολο αποκαλύπτεται κάθε ενότητα σε καθένα από τα ληφθέντα διαστήματα (όταν κάνετε μια λύση, μπορείτε να χρησιμοποιήσετε μια αριθμητική γραμμή, σημειώνοντας τα σημάδια σε αυτήν) 4). Η αρχική εξίσωση είναι ισοδύναμη με το σύνολο n+1 συστήματα, σε καθένα από τα οποία αναφέρεται η συμμετοχή της μεταβλητής Χένα από τα διαστήματα. Παραδείγματα: №1 . Λύστε την εξίσωση, στην απάντηση υποδείξτε τη μεγαλύτερη ρίζα:
ένας). Ας βρούμε τα μηδενικά των παραστάσεων υπομονάδας: x = 2; x = -3 2). Σημειώνουμε τις τιμές που βρέθηκαν στην αριθμητική γραμμή και προσδιορίζουμε με ποιο πρόσημο αποκαλύπτεται κάθε ενότητα στα διαστήματα που λαμβάνονται:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- δεν υπάρχουν λύσεις Η εξίσωση έχει δύο ρίζες. Απάντηση: η μεγαλύτερη ρίζα είναι x = 2. №2. Λύστε την εξίσωση, γράψτε ολόκληρη τη ρίζα στην απάντηση:
ένας). Ας βρούμε τα μηδενικά των παραστάσεων υπομονάδας: x = 1,5; x = - 1 2). Σημειώνουμε τις τιμές που βρέθηκαν στην αριθμητική γραμμή και καθορίζουμε με ποιο σύμβολο αποκαλύπτεται κάθε ενότητα στα ληφθέντα διαστήματα: x + 1 x + 1 x + 1 - + +
-1 1,5 х 2х – 3 2х – 3 2х – 3 - - +
3).
Το τελευταίο σύστημα δεν έχει λύσεις, επομένως, η εξίσωση έχει δύο ρίζες. Κατά την επίλυση της εξίσωσης, θα πρέπει να δώσετε προσοχή στο σύμβολο "-" μπροστά από τη δεύτερη ενότητα. Απάντηση: ακέραια ρίζα x = 7. №3. Λύστε την εξίσωση, στην απάντηση να αναφέρετε το άθροισμα των ριζών: 1). Ας βρούμε τα μηδενικά των παραστάσεων υπομονάδας: x = 5; x = 1; x = - 2 2). Σημειώνουμε τις τιμές που βρέθηκαν στην αριθμητική γραμμή και καθορίζουμε με ποιο σύμβολο αποκαλύπτεται κάθε ενότητα στα διαστήματα που λήφθηκαν: x - 5 x - 5 x - 5 x - 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Η εξίσωση έχει δύο ρίζες x = 0 και 2. Απάντηση: το άθροισμα των ριζών είναι 2. №4 . Λύστε την εξίσωση: 1). Ας βρούμε τα μηδενικά των παραστάσεων υπομονάδας: x = 1; x = 2; x = 3. 2). Ας προσδιορίσουμε το πρόσημο με το οποίο επεκτείνεται κάθε ενότητα στα ληφθέντα διαστήματα. 3).
Ας συνδυάσουμε λύσεις τρία πρώτασυστήματα. Απάντηση: ; x = 5.
Γυμνάσια: №24. Λύστε την εξίσωση:
№25. Λύστε την εξίσωση, στην απάντηση γράψτε το άθροισμα των ριζών: №26. Λύστε την εξίσωση, στην απάντηση υποδείξτε τη μικρότερη ρίζα: №27. Λύστε την εξίσωση, δώστε τη μεγαλύτερη ρίζα στην απάντησή σας:

Ενότητα 9. Εξισώσεις που περιέχουν πολλαπλές ενότητες

Οι εξισώσεις που περιέχουν πολλαπλές ενότητες υποθέτουν την παρουσία απόλυτων τιμών σε εκφράσεις υπομονάδας. Η βασική αρχή της επίλυσης εξισώσεων αυτού του τύπου είναι η διαδοχική αποκάλυψη ενοτήτων, ξεκινώντας από το "εξωτερικό". Κατά τη διάρκεια της λύσης, χρησιμοποιούνται οι τεχνικές που συζητούνται στις ενότητες Νο. 1, Νο. 3.

Παραδείγματα: №1. Λύστε την εξίσωση:
Απάντηση: x = 1; - έντεκα. №2. Λύστε την εξίσωση:
Απάντηση: x = 0; τέσσερα? - τέσσερα. №3. Λύστε την εξίσωση, στην απάντηση να αναφέρετε το γινόμενο των ριζών:
Απάντηση: Το γινόμενο των ριζών είναι 8. №4. Λύστε την εξίσωση:
Να χαρακτηρίσετε τις εξισώσεις του πληθυσμού (1) και (2) και εξετάστε τη λύση καθενός από αυτά ξεχωριστά για την ευκολία του σχεδιασμού. Δεδομένου ότι και οι δύο εξισώσεις περιέχουν περισσότερες από μία μονάδες, είναι πιο βολικό να πραγματοποιηθεί μια ισοδύναμη μετάβαση σε σύνολα συστημάτων. (1)

(2)


Απάντηση:
Γυμνάσια: №36. Λύστε την εξίσωση, στην απάντηση υποδείξτε το άθροισμα των ριζών: 5 │3x-5│ \u003d 25 x №37. Λύστε την εξίσωση, αν υπάρχουν περισσότερες από μία ρίζες, στην απάντηση να αναφέρετε το άθροισμα των ριζών: │x + 2│ x - 3x - 10 = 1 №38. Λύστε την εξίσωση: 3 │2x -4│ \u003d 9 │x│ №39. Λύστε την εξίσωση, στην απάντηση υποδείξτε τον αριθμό των ριζών για: 2 │ sin x │ = √2 №40 . Λύστε την εξίσωση, στην απάντηση υποδείξτε τον αριθμό των ριζών:

Ενότητα 3. Λογαριθμικές εξισώσεις.

Πριν λύσουμε τις παρακάτω εξισώσεις, είναι απαραίτητο να αναθεωρήσουμε τις ιδιότητες των λογαρίθμων και τη λογαριθμική συνάρτηση. Παραδείγματα: №1. Λύστε την εξίσωση, στην απάντηση υποδείξτε το γινόμενο των ριζών: log 2 (x + 1) 2 + log 2 │x + 1 │ \u003d 6 O.D.Z. x+1≠0 x≠ - 1

Περίπτωση 1: αν x ≥ - 1, τότε log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – ικανοποιεί τη συνθήκη x ≥ - 1 2 περίπτωση: αν x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – ικανοποιεί την συνθήκη x - 1
Απάντηση: Το γινόμενο των ριζών είναι 15.
№2. Λύστε την εξίσωση, στην απάντηση να αναφέρετε το άθροισμα των ριζών: lg
Ο Ο.Δ.Ζ.

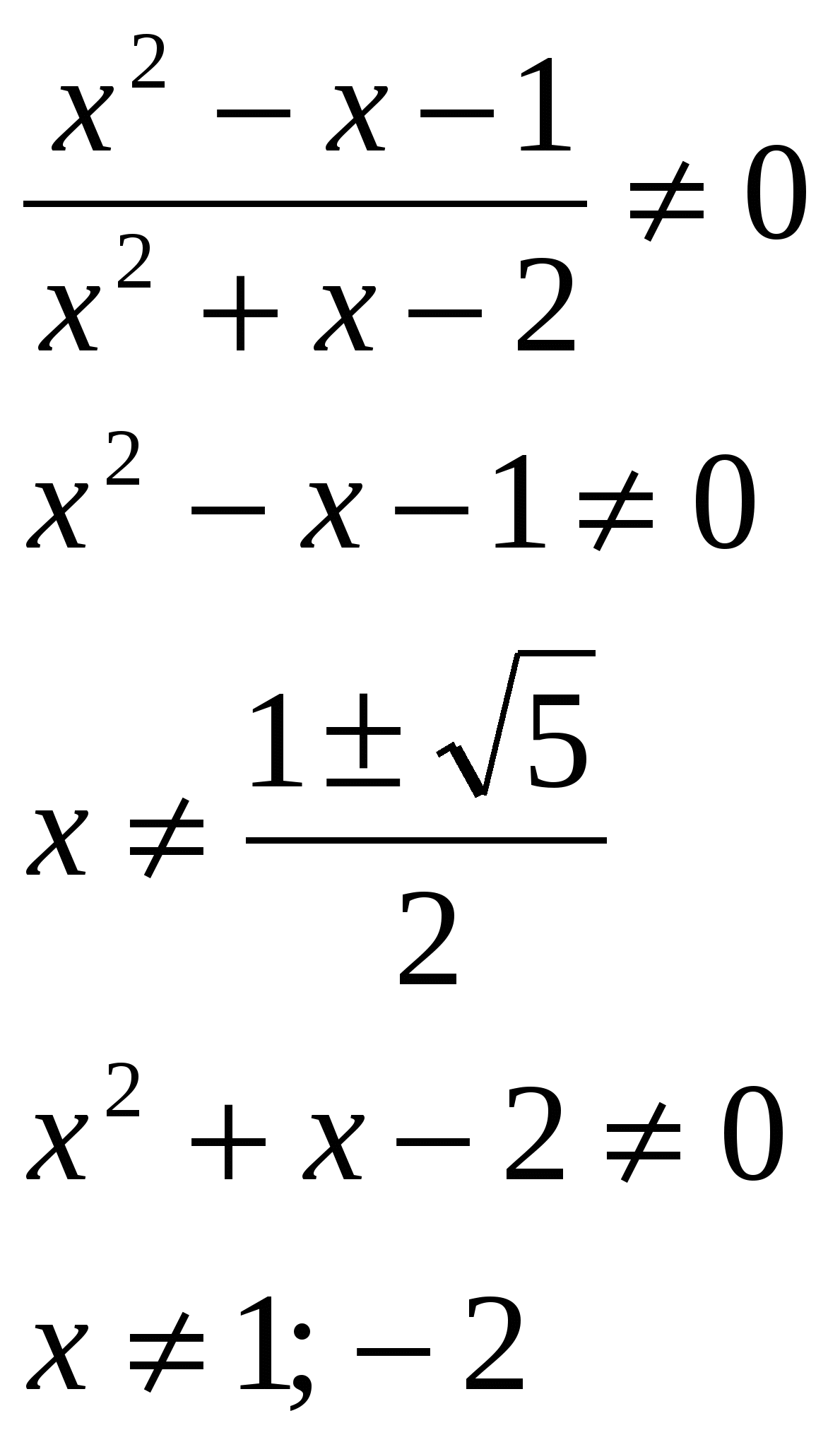
Απάντηση: το άθροισμα των ριζών είναι 0,5.
№3. Λύστε την εξίσωση: log 5
Ο Ο.Δ.Ζ.

Απάντηση: x = 9. №4. Λύστε την εξίσωση: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ Ο.Δ.Ζ. x > 0 Ας χρησιμοποιήσουμε τον τύπο για μετάβαση σε άλλη βάση. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Ας βρούμε τα μηδενικά των παραστάσεων υπομονάδας: x = 25; x \u003d Αυτοί οι αριθμοί διαιρούν την περιοχή των επιτρεπόμενων τιμών σε τρία διαστήματα, επομένως η εξίσωση είναι ισοδύναμη με το σύνολο τριών συστημάτων.
Απάντηση :)