Είναι απολύτως αδύνατο να λυθούν φυσικά προβλήματα ή παραδείγματα στα μαθηματικά χωρίς γνώση της παραγώγου και των μεθόδων υπολογισμού της. Η παράγωγος είναι μια από τις πιο σημαντικές έννοιες της μαθηματικής ανάλυσης. Αποφασίσαμε να αφιερώσουμε το σημερινό άρθρο σε αυτό το θεμελιώδες θέμα. Τι είναι παράγωγο, ποια είναι η φυσική του και γεωμετρική αίσθησηΠώς να υπολογίσετε την παράγωγο μιας συνάρτησης; Όλες αυτές οι ερωτήσεις μπορούν να συνδυαστούν σε μία: πώς να κατανοήσουμε την παράγωγο;

Γεωμετρική και φυσική σημασία της παραγώγου

Ας υπάρχει μια συνάρτηση f(x) , δίνεται σε κάποιο διάστημα (α, β) . Τα σημεία x και x0 ανήκουν σε αυτό το διάστημα. Όταν το x αλλάζει, αλλάζει και η ίδια η συνάρτηση. Αλλαγή επιχειρημάτων - διαφορά των τιμών του x-x0 . Αυτή η διαφορά γράφεται ως δέλτα χ και ονομάζεται προσαύξηση ορίσματος. Η αλλαγή ή η αύξηση μιας συνάρτησης είναι η διαφορά μεταξύ των τιμών της συνάρτησης σε δύο σημεία. Ορισμός παραγώγου:

Η παράγωγος μιας συνάρτησης σε ένα σημείο είναι το όριο του λόγου της αύξησης της συνάρτησης σε ένα δεδομένο σημείο προς την αύξηση του ορίσματος όταν το τελευταίο τείνει στο μηδέν.

Διαφορετικά μπορεί να γραφτεί ως εξής:

Τι νόημα έχει να βρεις ένα τέτοιο όριο; Ποιο όμως:

η παράγωγος μιας συνάρτησης σε ένα σημείο είναι ίση με την εφαπτομένη της γωνίας μεταξύ του άξονα OX και της εφαπτομένης στη γραφική παράσταση της συνάρτησης σε ένα δεδομένο σημείο.

Η φυσική σημασία του παραγώγου: η χρονική παράγωγος της διαδρομής είναι ίση με την ταχύτητα της ευθύγραμμης κίνησης.

Πράγματι, από τα σχολικά χρόνια, όλοι γνωρίζουν ότι η ταχύτητα είναι ένα ιδιωτικό μονοπάτι. x=f(t) και του χρόνου t . Μέση ταχύτητα για μια συγκεκριμένη χρονική περίοδο:

Για να μάθετε την ταχύτητα κίνησης κάθε φορά t0 πρέπει να υπολογίσετε το όριο:

Κανόνας πρώτος: βγάλτε τη σταθερά

Η σταθερά μπορεί να αφαιρεθεί από το πρόσημο της παραγώγου. Επιπλέον, πρέπει να γίνει. Όταν λύνετε παραδείγματα στα μαθηματικά, λάβετε κατά κανόνα - αν μπορείτε να απλοποιήσετε την έκφραση, φροντίστε να απλοποιήσετε .

Παράδειγμα. Ας υπολογίσουμε την παράγωγο:

Κανόνας δεύτερος: παράγωγος του αθροίσματος των συναρτήσεων

Η παράγωγος του αθροίσματος δύο συναρτήσεων είναι ίση με το άθροισμα των παραγώγων αυτών των συναρτήσεων. Το ίδιο ισχύει και για την παράγωγο της διαφοράς των συναρτήσεων.

Δεν θα δώσουμε μια απόδειξη αυτού του θεωρήματος, αλλά θα εξετάσουμε μάλλον ένα πρακτικό παράδειγμα.

Βρείτε την παράγωγο μιας συνάρτησης:

Τρίτος κανόνας: η παράγωγος του γινομένου των συναρτήσεων

Η παράγωγος του γινομένου δύο διαφοροποιήσιμων συναρτήσεων υπολογίζεται με τον τύπο:

Παράδειγμα: βρείτε την παράγωγο μιας συνάρτησης:

Λύση:

Εδώ είναι σημαντικό να πούμε για τον υπολογισμό των παραγώγων μιγαδικών συναρτήσεων. Η παράγωγος μιας μιγαδικής συνάρτησης είναι ίση με το γινόμενο της παραγώγου αυτής της συνάρτησης σε σχέση με το ενδιάμεσο όρισμα από την παράγωγο του ενδιάμεσου ορίσματος ως προς την ανεξάρτητη μεταβλητή.

Στο παραπάνω παράδειγμα, συναντάμε την έκφραση:

Σε αυτήν την περίπτωση, το ενδιάμεσο όρισμα είναι 8x στην πέμπτη δύναμη. Για να υπολογίσουμε την παράγωγο μιας τέτοιας έκφρασης, εξετάζουμε πρώτα την παράγωγο της εξωτερικής συνάρτησης σε σχέση με το ενδιάμεσο όρισμα και στη συνέχεια πολλαπλασιάζουμε με την παράγωγο του ίδιου του ενδιάμεσου ορίσματος σε σχέση με την ανεξάρτητη μεταβλητή.

Κανόνας Τέταρτος: Η παράγωγος του πηλίκου δύο συναρτήσεων

Τύπος για τον προσδιορισμό της παραγώγου ενός πηλίκου δύο συναρτήσεων:

Προσπαθήσαμε να μιλήσουμε για παράγωγα για ομοιώματα από την αρχή. Αυτό το θέμα δεν είναι τόσο απλό όσο ακούγεται, γι' αυτό προειδοποιήστε: υπάρχουν συχνά παγίδες στα παραδείγματα, επομένως να είστε προσεκτικοί κατά τον υπολογισμό των παραγώγων.

Για οποιαδήποτε ερώτηση σχετικά με αυτό και άλλα θέματα, μπορείτε να επικοινωνήσετε με τη φοιτητική υπηρεσία. Ανά βραχυπρόθεσμαθα σας βοηθήσουμε να λύσετε το πιο δύσκολο τεστ και να ασχοληθείτε με εργασίες, ακόμα κι αν δεν έχετε ασχοληθεί ποτέ με τον υπολογισμό των παραγώγων στο παρελθόν.

Στο πρόβλημα Β9 δίνεται μια γραφική παράσταση συνάρτησης ή παραγώγου, από την οποία απαιτείται να προσδιοριστεί μία από τις ακόλουθες ποσότητες:

1. Η τιμή της παραγώγου σε κάποιο σημείο x 0,
2. Υψηλά ή χαμηλά σημεία (ακραία σημεία),
3. Διαστήματα αύξουσας και φθίνουσας συνάρτησης (διαστήματα μονοτονίας).

Οι συναρτήσεις και οι παράγωγοι που παρουσιάζονται σε αυτό το πρόβλημα είναι πάντα συνεχείς, γεγονός που απλοποιεί πολύ τη λύση. Παρά το γεγονός ότι η εργασία ανήκει στο τμήμα της μαθηματικής ανάλυσης, είναι αρκετά στη δύναμη ακόμη και των πιο αδύναμων μαθητών, αφού εδώ δεν απαιτούνται βαθιές θεωρητικές γνώσεις.

Για να βρείτε την τιμή της παραγώγου, των ακραίων σημείων και των διαστημάτων μονοτονίας, υπάρχουν απλοί και καθολικοί αλγόριθμοι - όλοι θα συζητηθούν παρακάτω.

Διαβάστε προσεκτικά την κατάσταση του προβλήματος Β9 για να μην κάνετε ανόητα λάθη: μερικές φορές συναντώνται αρκετά ογκώδη κείμενα, αλλά υπάρχουν λίγες σημαντικές συνθήκες που επηρεάζουν την πορεία της λύσης.

Υπολογισμός της τιμής της παραγώγου. Μέθοδος δύο σημείων

Αν στο πρόβλημα δοθεί μια γραφική παράσταση της συνάρτησης f(x), εφαπτομένη σε αυτό το γράφημα σε κάποιο σημείο x 0 , και απαιτείται να βρεθεί η τιμή της παραγώγου σε αυτό το σημείο, εφαρμόζεται ο ακόλουθος αλγόριθμος:

1. Βρείτε δύο «επαρκή» σημεία στο γράφημα της εφαπτομένης: οι συντεταγμένες τους πρέπει να είναι ακέραιες. Ας συμβολίσουμε αυτά τα σημεία ως A (x 1 , y 1) και B (x 2 , y 2). Γράψτε σωστά τις συντεταγμένες - αυτό είναι βασική στιγμήλύσεις, και οποιοδήποτε λάθος εδώ οδηγεί σε λάθος απάντηση.
2. Γνωρίζοντας τις συντεταγμένες, είναι εύκολο να υπολογίσουμε την αύξηση του ορίσματος Δx = x 2 − x 1 και την αύξηση της συνάρτησης Δy = y 2 − y 1 .
3. Τέλος, βρίσκουμε την τιμή της παραγώγου D = Δy/Δx. Με άλλα λόγια, πρέπει να διαιρέσετε την αύξηση της συνάρτησης με την αύξηση του ορίσματος - και αυτή θα είναι η απάντηση.

Για άλλη μια φορά, σημειώνουμε: τα σημεία Α και Β πρέπει να αναζητηθούν ακριβώς στην εφαπτομένη και όχι στη γραφική παράσταση της συνάρτησης f(x), όπως συμβαίνει συχνά. Η εφαπτομένη θα περιέχει αναγκαστικά τουλάχιστον δύο τέτοια σημεία, διαφορετικά το πρόβλημα διατυπώνεται εσφαλμένα.

Θεωρήστε τα σημεία A (−3; 2) και B (−1; 6) και βρείτε τις προσαυξήσεις:
Δx \u003d x 2 - x 1 \u003d -1 - (-3) \u003d 2; Δy \u003d y 2 - y 1 \u003d 6 - 2 \u003d 4.

Ας βρούμε την τιμή της παραγώγου: D = Δy/Δx = 4/2 = 2.

Μια εργασία. Το σχήμα δείχνει τη γραφική παράσταση της συνάρτησης y \u003d f (x) και την εφαπτομένη σε αυτήν στο σημείο με την τετμημένη x 0. Να βρείτε την τιμή της παραγώγου της συνάρτησης f(x) στο σημείο x 0 .

Εξετάστε τα σημεία Α (0; 3) και Β (3; 0), βρείτε προσαυξήσεις:
Δx \u003d x 2 - x 1 \u003d 3 - 0 \u003d 3; Δy \u003d y 2 - y 1 \u003d 0 - 3 \u003d -3.

Τώρα βρίσκουμε την τιμή της παραγώγου: D = Δy/Δx = −3/3 = −1.

Μια εργασία. Το σχήμα δείχνει τη γραφική παράσταση της συνάρτησης y \u003d f (x) και την εφαπτομένη σε αυτήν στο σημείο με την τετμημένη x 0. Να βρείτε την τιμή της παραγώγου της συνάρτησης f(x) στο σημείο x 0 .

Εξετάστε τα σημεία Α (0; 2) και Β (5; 2) και βρείτε προσαυξήσεις:
Δx \u003d x 2 - x 1 \u003d 5 - 0 \u003d 5; Δy = y 2 - y 1 = 2 - 2 = 0.

Μένει να βρούμε την τιμή της παραγώγου: D = Δy/Δx = 0/5 = 0.

Από το τελευταίο παράδειγμα, μπορούμε να διατυπώσουμε τον κανόνα: εάν η εφαπτομένη είναι παράλληλη προς τον άξονα OX, η παράγωγος της συνάρτησης στο σημείο επαφής είναι ίση με μηδέν. Σε αυτήν την περίπτωση, δεν χρειάζεται καν να υπολογίσετε τίποτα - απλώς κοιτάξτε το γράφημα.

Υπολογισμός υψηλών και χαμηλών πόντων

Μερικές φορές αντί για γράφημα μιας συνάρτησης στο πρόβλημα Β9, δίνεται ένα γράφημα παραγώγου και απαιτείται να βρεθεί το μέγιστο ή το ελάχιστο σημείο της συνάρτησης. Σε αυτό το σενάριο, η μέθοδος των δύο σημείων είναι άχρηστη, αλλά υπάρχει ένας άλλος, ακόμη πιο απλός αλγόριθμος. Αρχικά, ας ορίσουμε την ορολογία:

1. Το σημείο x 0 ονομάζεται μέγιστο σημείο της συνάρτησης f(x) αν σε κάποια γειτονιά αυτού του σημείου ισχύει η ακόλουθη ανισότητα: f(x 0) ≥ f(x).
2. Το σημείο x 0 ονομάζεται ελάχιστο σημείο της συνάρτησης f(x) αν σε κάποια γειτονιά αυτού του σημείου ισχύει η ακόλουθη ανίσωση: f(x 0) ≤ f(x).

Για να βρείτε τα μέγιστα και ελάχιστα σημεία στο γράφημα της παραγώγου, αρκεί να εκτελέσετε τα ακόλουθα βήματα:

1. Ξανασχεδιάστε το γράφημα της παραγώγου, αφαιρώντας όλες τις περιττές πληροφορίες. Όπως δείχνει η πρακτική, τα επιπλέον δεδομένα παρεμβαίνουν μόνο στη λύση. Επομένως, σημειώνουμε τα μηδενικά της παραγώγου στον άξονα συντεταγμένων - και αυτό είναι.
2. Βρείτε τα σημάδια της παραγώγου στα διαστήματα μεταξύ των μηδενικών. Αν για κάποιο σημείο x 0 είναι γνωστό ότι f'(x 0) ≠ 0, τότε μόνο δύο επιλογές είναι δυνατές: f'(x 0) ≥ 0 ή f'(x 0) ≤ 0. Το πρόσημο της παραγώγου είναι εύκολο να προσδιοριστεί από το αρχικό σχέδιο: αν το γράφημα της παραγώγου βρίσκεται πάνω από τον άξονα OX, τότε f'(x) ≥ 0. Αντίθετα, εάν το γράφημα της παραγώγου βρίσκεται κάτω από τον άξονα OX, τότε f'(x) ≤ 0.
3. Ελέγχουμε ξανά τα μηδενικά και τα πρόσημα της παραγώγου. Όπου το πρόσημο αλλάζει από μείον σε συν, υπάρχει ένα ελάχιστο σημείο. Αντίστροφα, αν το πρόσημο της παραγώγου αλλάξει από συν σε πλην, αυτό είναι το μέγιστο σημείο. Η καταμέτρηση γίνεται πάντα από αριστερά προς τα δεξιά.

Αυτό το σχήμα λειτουργεί μόνο για συνεχείς συναρτήσεις - δεν υπάρχουν άλλες στο πρόβλημα Β9.

Μια εργασία. Το σχήμα δείχνει ένα γράφημα της παραγώγου της συνάρτησης f(x) που ορίζεται στο τμήμα [−5; 5]. Βρείτε το ελάχιστο σημείο της συνάρτησης f(x) σε αυτό το τμήμα.

Ας απαλλαγούμε από περιττές πληροφορίες - θα αφήσουμε μόνο τα σύνορα [−5; 5] και τα μηδενικά της παραγώγου x = −3 και x = 2,5. Σημειώστε επίσης τα σημάδια:

Προφανώς, στο σημείο x = −3, το πρόσημο της παραγώγου αλλάζει από μείον σε συν. Αυτό είναι το ελάχιστο σημείο.

Μια εργασία. Το σχήμα δείχνει μια γραφική παράσταση της παραγώγου της συνάρτησης f(x) που ορίζεται στο τμήμα [−3; 7]. Βρείτε το μέγιστο σημείο της συνάρτησης f(x) σε αυτό το τμήμα.

Ας ξανασχεδιάσουμε το γράφημα, αφήνοντας μόνο τα όρια [−3; 7] και τα μηδενικά της παραγώγου x = −1,7 και x = 5. Σημειώστε τα πρόσημα της παραγώγου στο γράφημα που προκύπτει. Εχουμε:

Προφανώς, στο σημείο x = 5, το πρόσημο της παραγώγου αλλάζει από συν σε πλην - αυτό είναι το μέγιστο σημείο.

Μια εργασία. Το σχήμα δείχνει ένα γράφημα της παραγώγου της συνάρτησης f(x) που ορίζεται στο τμήμα [−6; τέσσερα]. Βρείτε τον αριθμό των μέγιστων σημείων της συνάρτησης f(x), που ανήκουν στο τμήμα [−4; 3].

Από τις συνθήκες του προβλήματος προκύπτει ότι αρκεί να ληφθεί υπόψη μόνο το τμήμα του γραφήματος που οριοθετείται από το τμήμα [−4; 3]. Επομένως, χτίζουμε ένα νέο γράφημα, στο οποίο σημειώνουμε μόνο τα όρια [−4; 3] και τα μηδενικά της παραγώγου μέσα σε αυτό. Δηλαδή, τα σημεία x = −3,5 και x = 2. Παίρνουμε:

Σε αυτό το γράφημα, υπάρχει μόνο ένα μέγιστο σημείο x = 2. Είναι σε αυτό που το πρόσημο της παραγώγου αλλάζει από συν σε πλην.

Μια μικρή σημείωση για σημεία με μη ακέραιες συντεταγμένες. Για παράδειγμα, στο τελευταίο πρόβλημα, εξετάστηκε το σημείο x = −3,5, αλλά με την ίδια επιτυχία μπορούμε να πάρουμε x = −3,4. Εάν το πρόβλημα διατυπωθεί σωστά, τέτοιες αλλαγές δεν θα πρέπει να επηρεάζουν την απάντηση, καθώς τα σημεία "χωρίς σταθερό τόπο διαμονής" δεν εμπλέκονται άμεσα στην επίλυση του προβλήματος. Φυσικά, με ακέραιους πόντους ένα τέτοιο κόλπο δεν θα λειτουργήσει.

Εύρεση διαστημάτων αύξησης και μείωσης μιας συνάρτησης

Σε ένα τέτοιο πρόβλημα, όπως τα σημεία μέγιστου και ελαχίστου, προτείνεται να βρεθούν περιοχές στις οποίες η ίδια η συνάρτηση αυξάνεται ή μειώνεται από τη γραφική παράσταση της παραγώγου. Αρχικά, ας ορίσουμε τι είναι η αύξουσα και η φθίνουσα:

1. Μια συνάρτηση f(x) ονομάζεται αύξουσα σε ένα τμήμα εάν για οποιαδήποτε δύο σημεία x 1 και x 2 από αυτό το τμήμα η πρόταση είναι αληθής: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). Με άλλα λόγια, όσο μεγαλύτερη είναι η τιμή του ορίσματος, τόσο μεγαλύτερη είναι η τιμή της συνάρτησης.
2. Μια συνάρτηση f(x) ονομάζεται φθίνουσα σε ένα τμήμα εάν για οποιαδήποτε δύο σημεία x 1 και x 2 από αυτό το τμήμα η πρόταση είναι αληθής: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Εκείνοι. μεγαλύτερη αξίαΤο όρισμα αντιστοιχεί στη μικρότερη τιμή της συνάρτησης.

Διατυπώνουμε επαρκείς προϋποθέσεις για αύξηση και μείωση:

1. Για να αυξηθεί μια συνεχής συνάρτηση f(x) στο τμήμα , αρκεί η παράγωγός της μέσα στο τμήμα να είναι θετική, δηλ. f'(x) ≥ 0.
2. Για να μειωθεί μια συνεχής συνάρτηση f(x) στο τμήμα , αρκεί η παράγωγός της μέσα στο τμήμα να είναι αρνητική, δηλ. f'(x) ≤ 0.

Δεχόμαστε αυτούς τους ισχυρισμούς χωρίς απόδειξη. Έτσι, παίρνουμε ένα σχήμα για την εύρεση διαστημάτων αύξησης και μείωσης, το οποίο είναι από πολλές απόψεις παρόμοιο με τον αλγόριθμο για τον υπολογισμό των ακραίων σημείων:

1. Καταργήστε όλες τις περιττές πληροφορίες. Στο αρχικό γράφημα της παραγώγου, μας ενδιαφέρουν πρωτίστως τα μηδενικά της συνάρτησης, οπότε αφήνουμε μόνο αυτά.
2. Σημειώστε τα πρόσημα της παραγώγου στα διαστήματα μεταξύ των μηδενικών. Όπου f'(x) ≥ 0, η συνάρτηση αυξάνεται και όπου f'(x) ≤ 0, μειώνεται. Εάν το πρόβλημα έχει περιορισμούς στη μεταβλητή x, τους επισημαίνουμε επιπλέον στο νέο γράφημα.
3. Τώρα που γνωρίζουμε τη συμπεριφορά της συνάρτησης και τον περιορισμό, μένει να υπολογίσουμε την απαιτούμενη τιμή στο πρόβλημα.

Μια εργασία. Το σχήμα δείχνει μια γραφική παράσταση της παραγώγου της συνάρτησης f(x) που ορίζεται στο τμήμα [−3; 7.5]. Να βρείτε τα διαστήματα της φθίνουσας συνάρτησης f(x). Στην απάντησή σας, γράψτε το άθροισμα των ακεραίων που περιλαμβάνονται σε αυτά τα διαστήματα.

Ως συνήθως, ξανασχεδιάζουμε το γράφημα και σημειώνουμε τα όρια [−3; 7.5], καθώς και τα μηδενικά της παραγώγου x = −1.5 και x = 5.3. Στη συνέχεια σημειώνουμε τα σημάδια της παραγώγου. Εχουμε:

Εφόσον η παράγωγος είναι αρνητική στο διάστημα (− 1,5), αυτό είναι το διάστημα της φθίνουσας συνάρτησης. Απομένει να αθροίσουμε όλους τους ακέραιους αριθμούς που βρίσκονται μέσα σε αυτό το διάστημα:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Μια εργασία. Το σχήμα δείχνει ένα γράφημα της παραγώγου της συνάρτησης f(x) που ορίζεται στο τμήμα [−10; τέσσερα]. Να βρείτε τα διαστήματα της αύξουσας συνάρτησης f(x). Στην απάντησή σας, γράψτε το μήκος του μεγαλύτερου από αυτά.

Ας απαλλαγούμε από περιττές πληροφορίες. Αφήνουμε μόνο τα όρια [−10; 4] και μηδενικά της παραγώγου, που αυτή τη φορά αποδείχθηκαν τέσσερα: x = −8, x = −6, x = −3 και x = 2. Σημειώστε τα πρόσημα της παραγώγου και λάβετε την παρακάτω εικόνα:

Μας ενδιαφέρουν τα διαστήματα αύξησης της συνάρτησης, δηλ. όπου f'(x) ≥ 0. Υπάρχουν δύο τέτοια διαστήματα στη γραφική παράσταση: (−8; −6) και (−3; 2). Ας υπολογίσουμε το μήκος τους:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

Εφόσον απαιτείται να βρεθεί το μήκος του μεγαλύτερου από τα διαστήματα, γράφουμε την τιμή l 2 = 5 ως απάντηση.

Παράγωγο - κύρια έννοιαμαθηματική ανάλυση. Χαρακτηρίζει την αλλαγή στη συνάρτηση του επιχειρήματος Χσε κάποιο σημείο. Επιπλέον, το ίδιο το παράγωγο είναι συνάρτηση του επιχειρήματος Χ

Παράγωγη συνάρτηση σε ένα σημείο λέγεται το όριο (αν υπάρχει και είναι πεπερασμένο) του λόγου της αύξησης της συνάρτησης προς την αύξηση του ορίσματος, με την προϋπόθεση ότι η τελευταία τείνει στο μηδέν.

Τα πιο συνηθισμένα είναι τα παρακάτω παράγωγος συμβολισμός :

Παράδειγμα 1Εκμεταλλεύομαι ορισμός του παραγώγου, βρείτε την παράγωγο της συνάρτησης

Λύση. Από τον ορισμό της παραγώγου ακολουθεί το ακόλουθο σχήμα για τον υπολογισμό της.

Ας δώσουμε στο όρισμα μια αύξηση (δέλτα) και ας βρούμε την αύξηση της συνάρτησης:

Ας βρούμε τον λόγο της αύξησης της συνάρτησης προς την αύξηση του ορίσματος:

Ας υπολογίσουμε το όριο αυτού του λόγου υπό την προϋπόθεση ότι η αύξηση του ορίσματος τείνει στο μηδέν, δηλαδή την παράγωγο που απαιτείται στην συνθήκη του προβλήματος:

Η φυσική έννοια του παραγώγου

Προς την έννοια του παραγώγου οδήγησε τη μελέτη του Galileo Galilei για τον νόμο της ελεύθερης πτώσης των σωμάτων, και με μια ευρύτερη έννοια - το πρόβλημα της στιγμιαίας ταχύτητας της ανομοιόμορφης ευθύγραμμης κίνησης ενός σημείου.

Αφήστε το βότσαλο να σηκωθεί και στη συνέχεια να απελευθερωθεί από το υπόλοιπο. Μονοπάτι μικρόδιανυθεί στο χρόνο t, είναι συνάρτηση του χρόνου, δηλαδή. s = s(t). Εάν δοθεί ο νόμος κίνησης ενός σημείου, τότε είναι δυνατός ο προσδιορισμός της μέσης ταχύτητας για οποιαδήποτε χρονική περίοδο. Αφήστε τη στιγμή το βότσαλο να είναι στη θέση του ΕΝΑ, και αυτή τη στιγμή - στη θέση σι. Σε μια χρονική περίοδο (από tέως ) το σημείο έχει περάσει τη διαδρομή . Επομένως, η μέση ταχύτητα κίνησης για αυτό το χρονικό διάστημα, που συμβολίζουμε με , είναι

.

Ωστόσο, η κίνηση ενός σώματος που πέφτει ελεύθερα είναι σαφώς άνιση. Ταχύτητα vη πτώση αυξάνεται συνεχώς. Και μέση ταχύτηταδεν είναι πλέον αρκετό για να χαρακτηρίσει την ταχύτητα κίνησης σε διάφορα τμήματα του μονοπατιού. Αυτό το χαρακτηριστικό είναι όσο πιο ακριβές, τόσο μικρότερο είναι το χρονικό διάστημα. Επομένως, εισάγεται η ακόλουθη έννοια: στιγμιαία ταχύτητα ευθύγραμμης κίνησης (ή ταχύτητα μέσα αυτή τη στιγμήχρόνος t) ονομάζεται μέσο όριο ταχύτητας σε:

(με την προϋπόθεση ότι αυτό το όριο υπάρχει και είναι πεπερασμένο).

Αποδεικνύεται λοιπόν ότι η στιγμιαία ταχύτητα είναι το όριο του λόγου της αύξησης της συνάρτησης μικρό(t) στην αύξηση του ορίσματος t at Αυτό είναι το παράγωγο, το οποίο σε γενική εικόναγράφεται ως εξής:

.

Η λύση του καθορισμένου προβλήματος είναι φυσική έννοιαπαράγωγο . Άρα η παράγωγος της συνάρτησης y=f(Χ) στο σημείο Χκαλείται το όριο (αν υπάρχει και είναι πεπερασμένο) της αύξησης της συνάρτησης στην αύξηση του ορίσματος, με την προϋπόθεση ότι το τελευταίο τείνει στο μηδέν.

Παράδειγμα 2Να βρείτε την παράγωγο μιας συνάρτησης

Λύση. Από τον ορισμό της παραγώγου ακολουθεί το ακόλουθο σχήμα για τον υπολογισμό της.

Βήμα 1. Ας αυξήσουμε το όρισμα και ας βρούμε

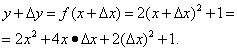
Βήμα 2. Βρείτε την αύξηση της συνάρτησης:

Βήμα 3. Βρείτε την αναλογία της αύξησης της συνάρτησης προς την αύξηση του ορίσματος:

Βήμα 4. Υπολογίστε το όριο αυτού του λόγου στο , δηλαδή την παράγωγο:

Η γεωμετρική σημασία της παραγώγου

Αφήστε τη συνάρτηση να οριστεί στο διάστημα και αφήστε το σημείο Μστη γραφική παράσταση της συνάρτησης αντιστοιχεί η τιμή του ορίσματος και το σημείο R- αξία . Περάστε μέσα από τις τελείες Μκαι Rγραμμή και καλέστε το διατέμνων. Δείξτε με τη γωνία μεταξύ της τομής και του άξονα. Προφανώς, αυτή η γωνία εξαρτάται από .

Αν υπάρχει

που διέρχεται από το σημείο ονομάζεται οριακή θέση της τομής ΚΥΡΙΟΣστο (ή στο).

Εφαπτομένη στη γραφική παράσταση μιας συνάρτησης σε ένα σημείο Μονομάζεται οριακή θέση του τμήματος ΚΥΡΙΟΣγια , ή, που είναι το ίδιο για .

Από τον ορισμό προκύπτει ότι για την ύπαρξη εφαπτομένης αρκεί να υπάρχει όριο

,

και το όριο ίσο με τη γωνίαη κλίση της εφαπτομένης στον άξονα.

Τώρα ας δώσουμε έναν ακριβή ορισμό της εφαπτομένης.

Εφαπτομένοςστη γραφική παράσταση μιας συνάρτησης σε ένα σημείο λέγεται ευθεία που διέρχεται από το σημείο και έχει κλίση, δηλ. ευθεία της οποίας η εξίσωση

Από αυτόν τον ορισμό προκύπτει ότι παράγωγο συνάρτησης ίση με την κλίση της εφαπτομένης στη γραφική παράσταση αυτής της συνάρτησης στο σημείο με την τετμημένη Χ. Αυτή είναι η γεωμετρική σημασία της παραγώγου.

Ο υπολογισμός της παραγώγου βρίσκεται συχνά στο ΧΡΗΣΗ Εργασιών. Αυτή η σελίδαπεριέχει μια λίστα τύπων για την εύρεση παραγώγων.

Κανόνες διαφοροποίησης

1. (k⋅f(x))′=k⋅f′(x).
2. (f(x)+g(x))′=f′(x)+g′(x).
3. (f(x)⋅ g(x))′=f′(x)⋅ g(x)+f(x)⋅ g′(x).
4. Παράγωγος μιγαδικής συνάρτησης. Αν y=F(u) και u=u(x), τότε καλείται η συνάρτηση y=f(x)=F(u(x)) σύνθετη λειτουργίααπό x. Ισούται με y′(x)=Fu′⋅ ux′.
5. Παράγωγο άρρητης συνάρτησης. Η συνάρτηση y=f(x) ονομάζεται άρρητη συνάρτηση που δίνεται από τη σχέση F(x,y)=0 αν F(x,f(x))≡0.
6. Παράγωγος της αντίστροφης συνάρτησης. Αν g(f(x))=x, τότε καλείται η συνάρτηση g(x). αντίστροφη συνάρτησηγια τη συνάρτηση y=f(x).
7. Παράγωγος παραμετρικά δεδομένης συνάρτησης. Έστω x και y ως συναρτήσεις της μεταβλητής t: x=x(t), y=y(t). Λέγεται ότι η y=y(x) είναι μια παραμετρικά καθορισμένη συνάρτηση στο διάστημα x∈ (a;b) αν σε αυτό το διάστημα η εξίσωση x=x(t) μπορεί να εκφραστεί ως t=t(x) και η συνάρτηση y=y( t(x))=y(x).
8. Παράγωγο δύναμης- εκθετικη συναρτηση. Βρίσκεται παίρνοντας τον λογάριθμο στη βάση του φυσικού λογάριθμου.

Σας συμβουλεύουμε να αποθηκεύσετε τον σύνδεσμο, καθώς αυτός ο πίνακας μπορεί να χρειαστεί πολλές φορές.
Ημερομηνία: 20/11/2014

Τι είναι ένα παράγωγο;

Πίνακας παραγώγων.

Η παράγωγος είναι μια από τις κύριες έννοιες των ανώτερων μαθηματικών. Σε αυτό το μάθημα, θα εισαγάγουμε αυτήν την έννοια. Ας γνωριστούμε, χωρίς αυστηρές μαθηματικές διατυπώσεις και αποδείξεις.

Αυτή η εισαγωγή θα σας επιτρέψει να:

Κατανοήστε την ουσία των απλών εργασιών με παράγωγο.

Επιλύστε με επιτυχία αυτές τις πολύ απλές εργασίες.

Προετοιμαστείτε για πιο σοβαρά μαθήματα παραγώγων.

Πρώτον, μια ευχάριστη έκπληξη.

Ο αυστηρός ορισμός της παραγώγου βασίζεται στη θεωρία των ορίων και το πράγμα είναι μάλλον περίπλοκο. Είναι αναστατωμένο. Αλλά η πρακτική εφαρμογή του παραγώγου, κατά κανόνα, δεν απαιτεί τόσο εκτεταμένη και βαθιά γνώση!

Για να ολοκληρώσετε με επιτυχία τις περισσότερες εργασίες στο σχολείο και στο πανεπιστήμιο, αρκεί να γνωρίζετε μόνο μερικούς όρους- να κατανοήσουν την εργασία, και μόνο μερικοί κανόνες- να το λύσω. Και αυτό είναι όλο. Αυτό με κάνει χαρούμενο.

Θα γνωριστούμε;)

Όροι και ονομασίες.

Υπάρχουν πολλές μαθηματικές πράξεις στα στοιχειώδη μαθηματικά. Πρόσθεση, αφαίρεση, πολλαπλασιασμός, εκθετικότητα, λογάριθμος κ.λπ. Εάν προστεθεί μία ακόμη πράξη σε αυτές τις πράξεις, τα στοιχειώδη μαθηματικά γίνονται υψηλότερα. Αυτή η νέα λειτουργία ονομάζεται ΔΙΑΦΟΡΕΤΙΚΟΤΗΤΑ-διάκριση.Ο ορισμός και η έννοια αυτής της λειτουργίας θα συζητηθούν σε ξεχωριστά μαθήματα.

Εδώ είναι σημαντικό να καταλάβουμε ότι η διαφοροποίηση είναι απλώς μια μαθηματική πράξη σε μια συνάρτηση. Αναλαμβάνουμε οποιαδήποτε λειτουργία και ορισμένους κανόνες, μεταμορφώστε το. Το αποτέλεσμα είναι μια νέα λειτουργία. Αυτή η νέα συνάρτηση ονομάζεται: παράγωγο.

ΔΙΑΦΟΡΕΤΙΚΟΤΗΤΑ-διάκριση- δράση σε μια λειτουργία.

Παράγωγοείναι το αποτέλεσμα αυτής της ενέργειας.

Όπως, για παράδειγμα, άθροισμαείναι το αποτέλεσμα της προσθήκης. Ή ιδιωτικόςείναι το αποτέλεσμα της διαίρεσης.

Γνωρίζοντας τους όρους, μπορείτε τουλάχιστον να κατανοήσετε τις εργασίες.) Η διατύπωση είναι η εξής: Βρείτε την παράγωγο μιας συνάρτησης. πάρε το παράγωγο? διαφοροποίηση της συνάρτησης. υπολογισμός παραγώγουκαι τα λοιπά. Είναι όλο ίδιο.Φυσικά, υπάρχουν πιο σύνθετες εργασίες, όπου η εύρεση της παραγώγου (διαφοροποίηση) θα είναι μόνο ένα από τα βήματα για την επίλυση της εργασίας.

Η παράγωγος συμβολίζεται με μια παύλα πάνω δεξιά πάνω από τη συνάρτηση. Σαν αυτό: y"ή f"(x)ή S"(t)και ούτω καθεξής.

ανάγνωση y εγκεφαλικό, ef εγκεφαλικό από x, es εγκεφαλικό από te,καλά κατάλαβες...)

Ένας πρώτος μπορεί επίσης να υποδηλώνει την παράγωγο μιας συγκεκριμένης συνάρτησης, για παράδειγμα: (2x+3)", (Χ 3 )" , (sinx)"και τα λοιπά. Συχνά η παράγωγος συμβολίζεται χρησιμοποιώντας διαφορικά, αλλά δεν θα εξετάσουμε μια τέτοια σημείωση σε αυτό το μάθημα.

Ας υποθέσουμε ότι έχουμε μάθει να κατανοούμε τις εργασίες. Δεν μένει τίποτα - για να μάθουμε πώς να τα λύσουμε.) Να σας υπενθυμίσω ξανά: η εύρεση της παραγώγου είναι μετασχηματισμός μιας συνάρτησης σύμφωνα με ορισμένους κανόνες.Αυτοί οι κανόνες είναι εκπληκτικά λίγοι.

Για να βρείτε την παράγωγο μιας συνάρτησης, χρειάζεται μόνο να γνωρίζετε τρία πράγματα. Τρεις πυλώνες στους οποίους στηρίζεται κάθε διαφοροποίηση. Εδώ είναι οι τρεις φάλαινες:

1. Πίνακας παραγώγων (τύποι διαφοροποίησης).

3. Παράγωγος μιγαδικής συνάρτησης.

Ας ξεκινήσουμε με τη σειρά. Σε αυτό το μάθημα, θα εξετάσουμε τον πίνακα των παραγώγων.

Πίνακας παραγώγων.

Ο κόσμος έχει άπειρο αριθμό λειτουργιών. Μεταξύ αυτού του συνόλου υπάρχουν λειτουργίες που είναι πιο σημαντικές για Πρακτική εφαρμογη. Αυτές οι λειτουργίες βρίσκονται σε όλους τους νόμους της φύσης. Από αυτές τις λειτουργίες, όπως και από τούβλα, μπορείτε να κατασκευάσετε όλες τις άλλες. Αυτή η κατηγορία συναρτήσεων ονομάζεται στοιχειώδεις λειτουργίες.Είναι αυτές οι συναρτήσεις που μελετώνται στο σχολείο - γραμμικές, τετραγωνικές, υπερβολές κ.λπ.

Διαφοροποίηση συναρτήσεων «από την αρχή», π.χ. με βάση τον ορισμό της παραγώγου και τη θεωρία των ορίων - πράγμα μάλλον χρονοβόρο. Και οι μαθηματικοί είναι άνθρωποι, ναι, ναι!) Απλοποίησαν λοιπόν τη ζωή τους (και εμάς). Υπολόγισαν παραγώγους στοιχειωδών συναρτήσεων πριν από εμάς. Το αποτέλεσμα είναι ένας πίνακας παραγώγων, όπου όλα είναι έτοιμα.)

Εδώ είναι, αυτό το πιάτο για τις πιο δημοφιλείς λειτουργίες. Αριστερά - στοιχειώδης λειτουργία, στα δεξιά είναι το παράγωγό του.

	Λειτουργία y	Παράγωγος συνάρτησης y y"
1	C (σταθερά)	C" = 0
2	Χ	x" = 1
3	x n (n είναι οποιοσδήποτε αριθμός)	(x n)" = nx n-1
	x 2 (n = 2)	(x 2)" = 2x
4	αμαρτία x	(sinx)" = cosx
	cos x	(cos x)" = - αμαρτία x
	tg x
	ctg x
5	arcsin x
	arccos x
	arctg x
	arcctg x
4	έναΧ
	μιΧ
5	κούτσουρο έναΧ
	ln x ( α = ε)

Συνιστώ να δώσετε προσοχή στην τρίτη ομάδα συναρτήσεων σε αυτόν τον πίνακα παραγώγων. Παράγωγο λειτουργία ισχύος- ένας από τους πιο συνηθισμένους τύπους, αν όχι ο πιο συνηθισμένος! Είναι σαφής η υπόδειξη;) Ναι, είναι επιθυμητό να γνωρίζουμε τον πίνακα των παραγώγων από καρδιάς. Παρεμπιπτόντως, αυτό δεν είναι τόσο δύσκολο όσο μπορεί να φαίνεται. Προσπαθήστε να λύσετε περισσότερα παραδείγματα, ο ίδιος ο πίνακας θα θυμάται!)

Η εύρεση της πινακοποιημένης τιμής της παραγώγου, όπως καταλαβαίνετε, δεν είναι η πιο δύσκολη δουλειά. Επομένως, πολύ συχνά σε τέτοιες εργασίες υπάρχουν πρόσθετες μάρκες. Είτε στη διατύπωση της εργασίας, είτε στην αρχική συνάρτηση, η οποία δεν φαίνεται να υπάρχει στον πίνακα ...

Ας δούμε μερικά παραδείγματα:

1. Να βρείτε την παράγωγο της συνάρτησης y = x 3

Δεν υπάρχει τέτοια λειτουργία στον πίνακα. Υπάρχει όμως μια γενική παράγωγος της συνάρτησης ισχύος (τρίτη ομάδα). Στην περίπτωσή μας, n=3. Αντικαθιστούμε λοιπόν το τριπλό αντί για n και γράφουμε προσεκτικά το αποτέλεσμα:

(Χ 3) " = 3 x 3-1 = 3x 2

Αυτό είναι το μόνο που υπάρχει σε αυτό.

Απάντηση: y" = 3x 2

2. Να βρείτε την τιμή της παραγώγου της συνάρτησης y = sinx στο σημείο x = 0.

Αυτή η εργασία σημαίνει ότι πρέπει πρώτα να βρείτε την παράγωγο του ημιτόνου και μετά να αντικαταστήσετε την τιμή x = 0σε αυτήν την ίδια παράγωγο. Είναι με αυτή τη σειρά!Διαφορετικά, συμβαίνει να αντικαταστήσουν αμέσως το μηδέν στην αρχική συνάρτηση ... Μας ζητείται να βρούμε όχι την τιμή της αρχικής συνάρτησης, αλλά την τιμή το παράγωγό του.Η παράγωγος, να σας υπενθυμίσω, είναι ήδη μια νέα συνάρτηση.

Στην πλάκα βρίσκουμε το ημίτονο και την αντίστοιχη παράγωγο:

y" = (sinx)" = cosx

Αντικαταστήστε το μηδέν στην παράγωγο:

y"(0) = cos 0 = 1

Αυτή θα είναι η απάντηση.

3. Διαφοροποιήστε τη συνάρτηση:

Τι εμπνέει;) Δεν υπάρχει καν τέτοια συνάρτηση στον πίνακα των παραγώγων.

Επιτρέψτε μου να σας υπενθυμίσω ότι για να διαφοροποιήσετε μια συνάρτηση είναι απλώς να βρείτε την παράγωγο αυτής της συνάρτησης. Εάν ξεχάσετε τη στοιχειώδη τριγωνομετρία, η εύρεση της παραγώγου της συνάρτησής μας είναι αρκετά ενοχλητική. Το τραπέζι δεν βοηθάει...

Αν όμως δούμε ότι η λειτουργία μας είναι συνημίτονο διπλή γωνία , τότε όλα γίνονται αμέσως καλύτερα!

Ναι ναι! Θυμηθείτε ότι ο μετασχηματισμός της αρχικής συνάρτησης πριν από τη διαφοροποίησηαρκετά αποδεκτό! Και συμβαίνει να κάνει τη ζωή πολύ πιο εύκολη. Σύμφωνα με τον τύπο για το συνημίτονο διπλής γωνίας:

Εκείνοι. η δύσκολη λειτουργία μας δεν είναι παρά y = κοκ. Και αυτή είναι μια συνάρτηση πίνακα. Λαμβάνουμε αμέσως:

Απάντηση: y" = - αμαρτία x.

Παράδειγμα για προχωρημένους πτυχιούχους και φοιτητές:

4. Βρείτε την παράγωγο μιας συνάρτησης:

Δεν υπάρχει τέτοια συνάρτηση στον πίνακα παραγώγων, φυσικά. Αλλά αν θυμάστε στοιχειώδη μαθηματικά, ενέργειες με δυνάμεις... Τότε είναι πολύ πιθανό να απλοποιήσετε αυτή τη συνάρτηση. Σαν αυτό:

Και το x στη δύναμη του ενός δέκατου είναι ήδη μια συνάρτηση πίνακα! Η τρίτη ομάδα, n=1/10. Απευθείας σύμφωνα με τον τύπο και γράψτε:

Αυτό είναι όλο. Αυτή θα είναι η απάντηση.

Ελπίζω ότι με την πρώτη φάλαινα της διαφοροποίησης - τον πίνακα των παραγώγων - όλα είναι ξεκάθαρα. Μένει να ασχοληθούμε με τις δύο εναπομείνασες φάλαινες. Στο επόμενο μάθημα, θα μάθουμε τους κανόνες της διαφοροποίησης.